啟蒙數學

 
動腦時間!

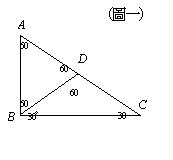
記的好像是第二次上課時, 我的學生恩問我如何邏輯推理? 他說“我可以解題,因為我只要把過程記住就行了. 如果題目必須無中生有的話,例如作補助線, 我就有問題了. 你能教我怎麼想嗎?” 我說“你是我教過幾千個學生中, 第一個要我教他怎麼想的人. 何況你才一個國中生, 我教過的學生大多數是大學或以上的學生. 不錯喔!”你有想懂甚麼樣的題目嗎?  他回覆沒有. 我就問恩: 如何證明60度直角三角形的邊長比率為1 : 根號(3) : 2? 他想一下後, 說他不會. “考試時, 你喜歡看到甚麼樣的三角形題目, 例如任意, 等腰, …” 我問. 他回覆,直角,等腰,和正三角形. (您想到的是不是跟恩的一樣的呢?)  我問他 “為甚麼呢?”  恩回覆, “那些三角形帶有特別的性質.”  我叫恩,試用他所知道三角形的性質來證明. 恩說, 能不能舉例. 我提示恩,在三角形的內部作補助線,來行成你喜歡的特別三角形. 恩想了一下說他會了. 請看他的解法:

今天我的學生楊,問我一個有關對數不等式的問題,
1 + log ₂(2x+1) > log ₄(4x – 1), 解x,
說他不會. 我跟往常一樣, 叫他出給他自己同一類型,簡單一點的問題.
他說 “1
> log ₄(4x – 1), 解x,可以嗎?”
我點頭說 “你應該會判斷才是阿!
你會解嗎?” 楊知道如果他不會的話,
我會叫他出一個更簡單一點的問題, 直到他會解為止. 如果他不會解的話, 他出下一更簡單一點的問題,
可能是1 > log ₄
x, 解x.
以下是他對 “1
> log ₄(4x – 1), 解x”
這個問題的解法:

| x |,  x以外的符號 |  | 是所謂的絕對值. 這表示不管x是一個正數或負數的值，取絕對值得結果是恆正. 例如 | x | = 1, 則 x = 1 或 x = -1,  | x | > 1, 則 x > 1 或 x < -1, 且 | x | < 1, 則 x < 1 或 x > -1. 從幾何的角來看, | x | < 1可解示成以x=0為中心點距離小於1的所有點的集合. 絕對值的題目可以蠻進階的. 例如求 | 3x + 1| > | x – 4 | 中x的範圍? 此問題的解答, 在本文章的最下面. 首先我們來討論如何從邏輯推理的角度來探討這個問題.            | x |, the symbol , |  |, outside of x is called the absolute value.  It means that no matter x is a negative or a positive value,| x | is always positive. For example, if | x | = 1 then x = 1 or x = -1,  | x | > 1 then x > 1 or x < -1, and  | x | < 1 then x < 1 or x > -1. Geometrically, | x | < 1 means that the set of all of points that the distance from the point x = 0 is less than 1.  The problems on the absolute value could get very advanced, for example, find the range of x for | 3x + 1| > | x – 4 |.  The answer of this problem is at bottom of this article. Now, let’s find the procedure that we can solve this problem logically.

微分定義: 設函數y = f(x)在某區間內,而x值為x0及x0 + Δx,其Δx值為無窮小時.在此區間內某兩無窮接近點的斜率, f(x)的微分為Δy / Δx = (f(x₀
+ Δx) - f(x₀))
/ (x₀ + Δx - x₀) = (f(x₀
+ Δx) - f(x₀))
/ Δx, Δx稱為自變數記作dx,即是dx = Δx. Δy稱為應變數記作dy,即是dy = Δy.於是一函數y = f(x)的微分(導數) = f'(x) = dy / dx.又可記作dy = f'(x) dx.

 如圖三角形的兩條高AD,BE一定交於一點 H,只要證明從C至H作一線交AB於F也是另一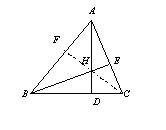條高就可以.
三角形ACD與三角形BCE相似 (為甚麼?)   Þ   三角形ACD,三角形BCE,三角形BDH 與三角形AEH全部相似(為甚麼?)   Þ   AE/EH=BE/CE  Þ  AE/ BE = EH /CE, 又ÐAEB= ÐCEB=90°   Þ  三角形ABE與三角形CEH相似  (為甚麼?)  Þ  ÐABE= ÐECH   又ÐEHC= ÐFHB (為甚麼?)     Þ   ÐHFB= ÐHEC=90°, 故 CF 亦是高.

解答提示: (第一類型如圖一)
            9=5,4 (不可能?)
            8=5,3 (不可能?)
x          7=5,2 (7,3); 4,3 (7,1) | 1,0 (1) ;如圖二和圖三所示

  幻方專家

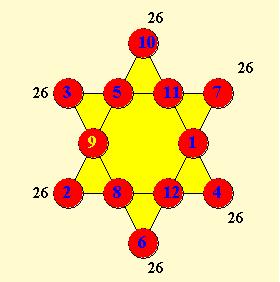
6階星形格式幻方或縱橫圖，由一組排放在6角星形交點的整數組成，其每4個數的行之和均相等為26。所填充的數是由從1到12的連續整數組成，其如上圖。其有80組解答，試試看您是否能找到所有解答.

 

連接到程式之前須知事項: (*須裝JVM 方可使用程式)

 

須用右滑鼠按鈕點圓圈按選1至 12 之一個數字或換數字.後鬆該滑鼠按鈕. 須用左滑鼠按鈕點按選一圓圈內的數字, 並移至另一圓圈內的數字位子, 後鬆該滑鼠按鈕,來交換數字.

 

New Game: 重新開始

Remove Current: 刪除剛填的數字(黃色)

Expert Help:  專家解題

 
和的夾角為q,則,並找其法向量,使此法向量與和兩向量垂直且此法向量的長度(量)為._(如圖七)
證: 由內積公式得,則,所以,因其為z方向的量故法向量為=(0,0, ). 則法向量的公式為. 法向量垂直於和,因 (0,0, )×(x₁,y₁,0)=0 和(0,0, )×(x₂,y₂,0)=0.
(1) 試證三度空間的外積公式及其法向量的關係式亦成立.
 

和的夾角為q,則,(如圖六) =(x₁,y₁), =(x₂,y₂); =(x₁,y₁)× (x₂,y₂)= x₁ x₂,+y₁ y_2.
 
證: 由餘弦定理得;由距離公式得=,比較(1)和(2)可得, 故定義
 (x₁,y₁)× (x₂,y₂)= x₁ x₂,+y₁ y_2­=_.
 
(1) Û  
(2) ,則=
(3) , 若, 的一垂直向量為(y₂,-x₂), 因(x₂, y₂)× (y₂,-x₂)= x₂ y₂- y₂ x₂=0, 所以(y₂,-x₂)平行於
(4) 證明在上之正射影為(),且正射影長為.